NVIDIA Hopper: H100 and FP8 Support
With the release of the NVIDIA H100 Tensor Core GPU, one of the most exciting features is the native support for FP8 data types. Compared to 16-bit floating-point on the H100, FP8 increases the delivered application performance by 2x, and reduces memory requirements by 2x. These new FP8 types can be used to speed up training or in post-training quantization (PTQ) to speed up inference.
FP8 Specification
In the whitepaper FP8 Formats for Deep Learning, authored by those at NVIDIA, Arm, and Intel, the 8-bit floating-point (FP8) specification is proposed for two formats: E4M3 and E5M2:
E5M2
range: -57344 to 57344
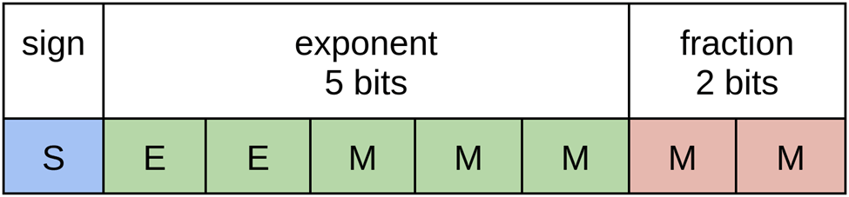
E5M2 follows the IEEE 754 conventions for representation of special values (NaN, Inf) used in higher-precision types (the smallest precision standardized by IEEE is FP16). One interesting point to note is that it contains the same number of exponent bits as FP16, and therefore offers a similar range, albeit with much less precision.
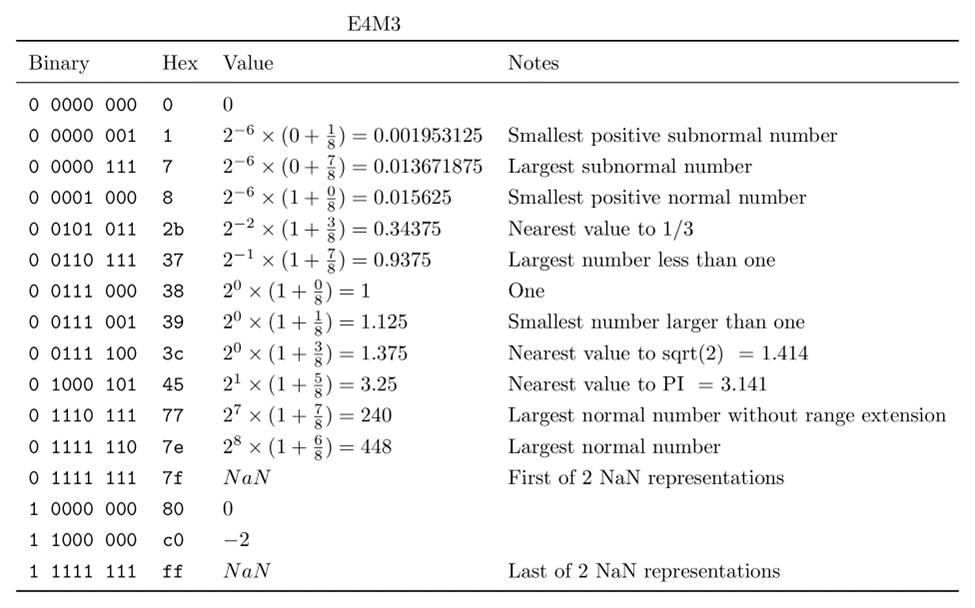
E4M3
range: -448 to 448
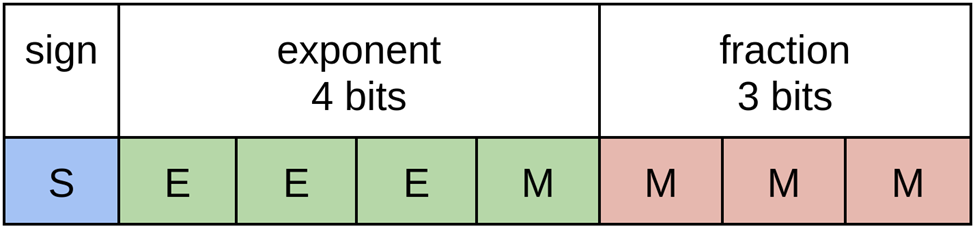
E4M3 trades one exponent bit for another fractional bit, increasing precision at the expense of range. Diverging slightly from IEEE 754 conventions for higher precision types, it is modified by removing infinity, and only contains two NaN values. This extends its range from (-240, 240) to (-480, 480), adding 14 additional representations after the modification.
E4M3 trades one exponent bit for another fractional bit, increasing precision at the expense of range. Diverging slightly from IEEE 754 conventions for higher precision types, it is modified by removing infinity, and only contains two NaN values. This extends its range from (-240, 240) to (-480, 480), adding 14 additional representations after the modification.
The recommended use of FP8 encodings is E4M3 for weight and activation tensors, and E5M2 for gradient tensors.
Why FP8?
Today’s state-of-the-art language models can contain billions of parameters. By moving from 16-bit floating point to FP8, we can reduce the memory requirements in half.
Even more exciting is the increase in throughput. Training in 16-bit floating point has already been shown to be greatly beneficial. Training in FP8 offers an even greater speedup. Results from the whitepaper are very promising, with all models reaching accuracy well within 1% of their 16-bit floating point baselines.
Increasing inference speed is the other use case. While models can currently be quantized to INT8, this process may require specialized training, or introduce unacceptable accuracy loss. By quantizing models to FP8, we are just moving from one floating point representation to another, which removes some of the complications of using 8-bit integers. Of course, models trained in FP8 do not require quantization, since training and inference precisions match.
FP8 Inference
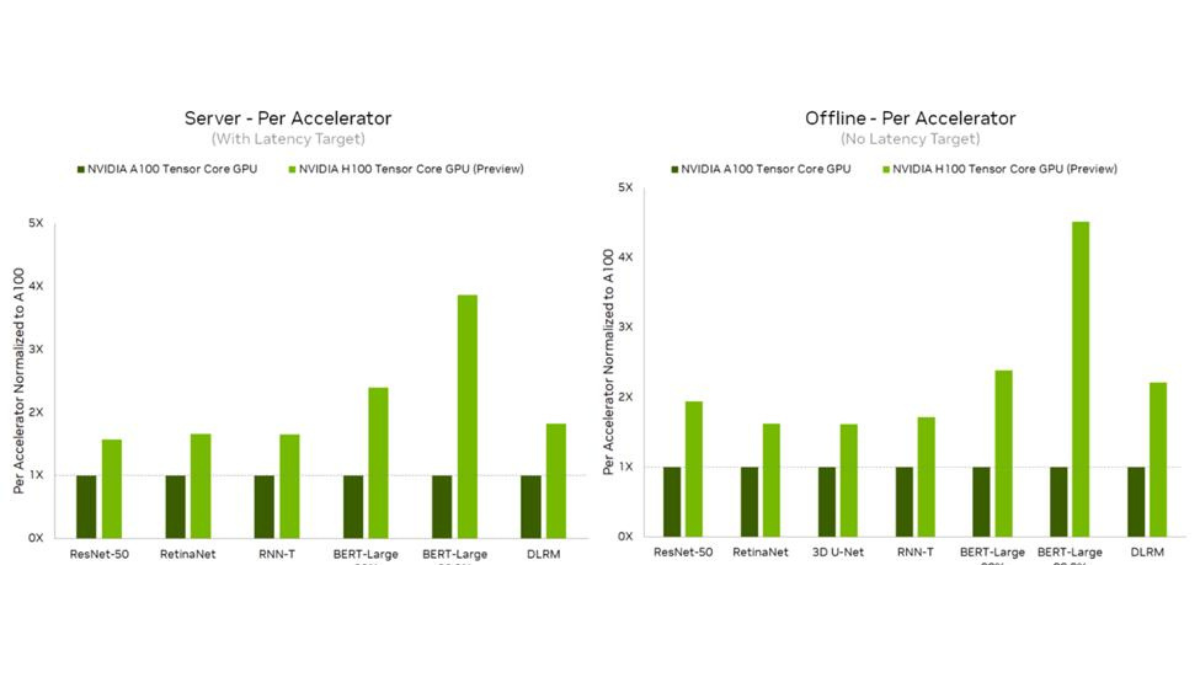
In the most recent MLPerf results, NVIDIA demonstrated up to 4.5x speedup in model inference performance on the NVIDIA H100 compared to previous results on the NVIDIA A100 Tensor Core GPU. Using the same data types, the H100 showed a 2x increase over the A100. Switching to FP8 resulted in yet another 2x increase in speed.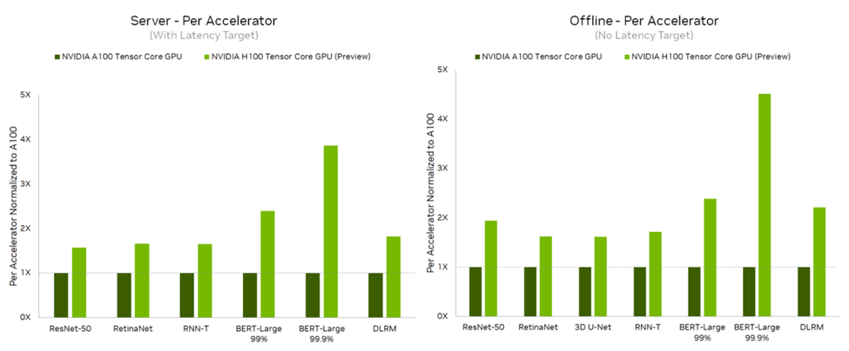
Currently, the only other 8-bit representation used for inference is INT8. This is often done by using post-training quantization (PTQ). However, this may result in a significant decrease in accuracy due to the vast difference between the native floating-point representation and INT8.
One common way to deal with this problem is quantization-aware training (QAT), which performs quantization on the forward-pass, in order to reduce the loss in accuracy during PTQ. Even with QAT, accuracy may still not be acceptable compared to the original model.
The results in the whitepaper show that a higher amount of accuracy is retained with FP8 PTQ, compared to INT8 PTQ. While this paper does not cover QAT results, in the paper FP8 Quantization: The Power of the Exponent, the authors show that QAT may also be used with FP8 to achieve even closer accuracy compared to the baseline model. However, the authors concluded that both formats performed similarly well with QAT.
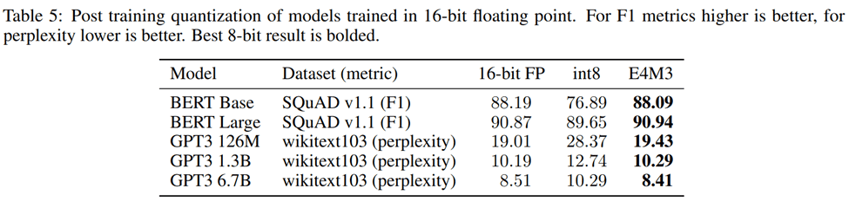
The conclusion we can derive from these results is that by switching to FP8, we can have more accurate models with just PTQ alone without needing to change our training code to use QAT, as is often the case with INT8 quantization.
Once support for FP8 comes to frameworks like PyTorch, TensorFlow, Onnx, and TensorRT, we expect to see this become the state-of-the-art method for quantizing models and boosting inference speed.
FP8 Training
As mentioned earlier, the potential benefits of reduced memory and increased throughput offer the potential for training larger models, as well as decreasing the time of training. With many ML researchers using cloud-based GPUs, such as the ones offered on Lambda GPU Cloud, being able to use half as many GPUs, or training in half the time, can directly result in significant cost savings on your bill!
The main concern with training with smaller representations is accuracy. As with inference, the results from the whitepaper show these to be quite good compared to their baselines:
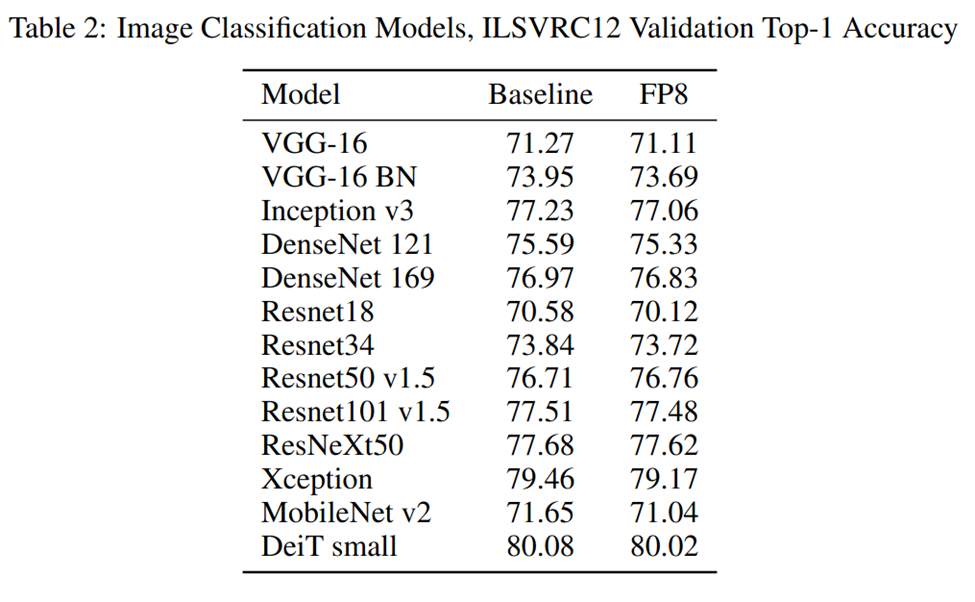
Large language models showed very promising results as well (lower perplexity is better):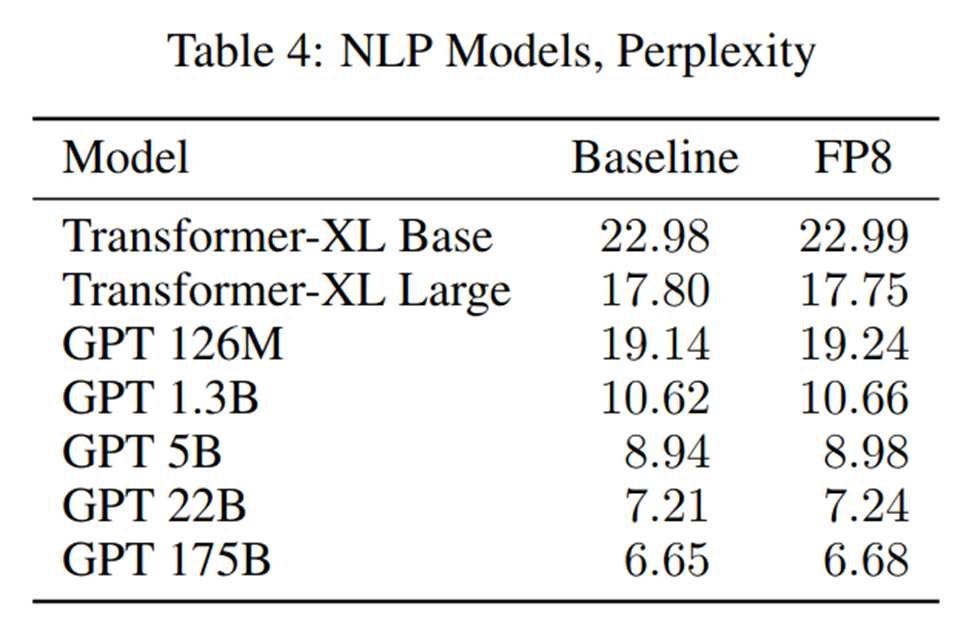
As with inference, while the H100 hardware supports FP8, support from frameworks like PyTorch and TensorFlow is coming soon, and once it it arrives, we can start training models ourselves in FP8.
FP8 - More Details
For those that are curious, here’s some more information about the two FP8 representations, and what they look like: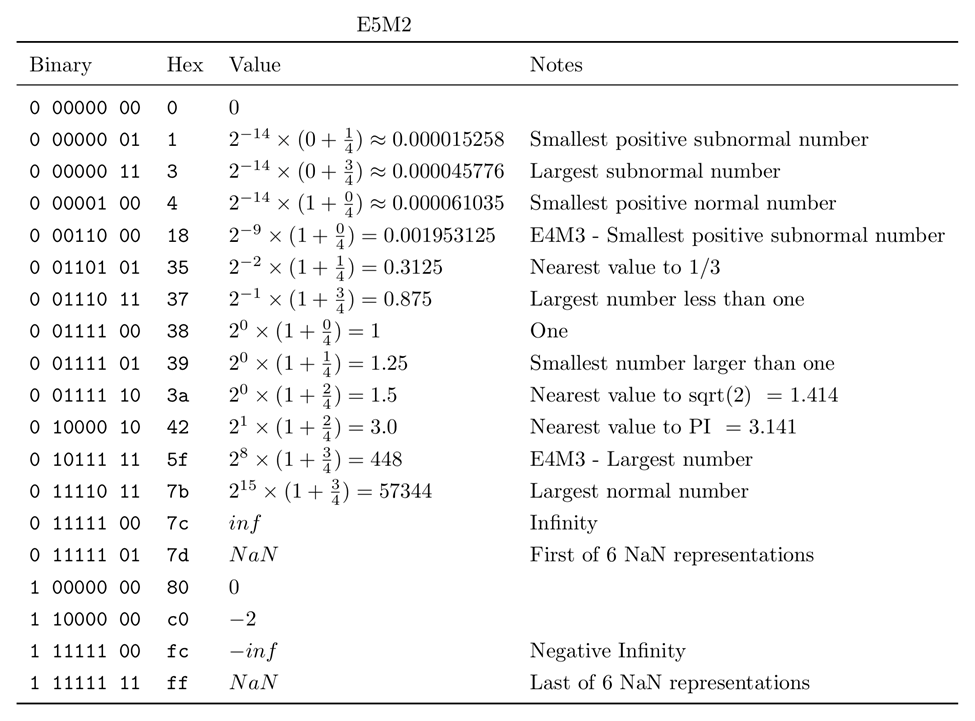
Here we show how positive ranges of E4M3 and E5M2 differ, when viewed on a log scale.
One thing to note is that of the 122 possible positive numbers in E5M2, 72 are within the range of E4M3, with only 23 numbers less than the smallest positive value in E4M3, and 28 numbers larger than the largest positive value in E4M3.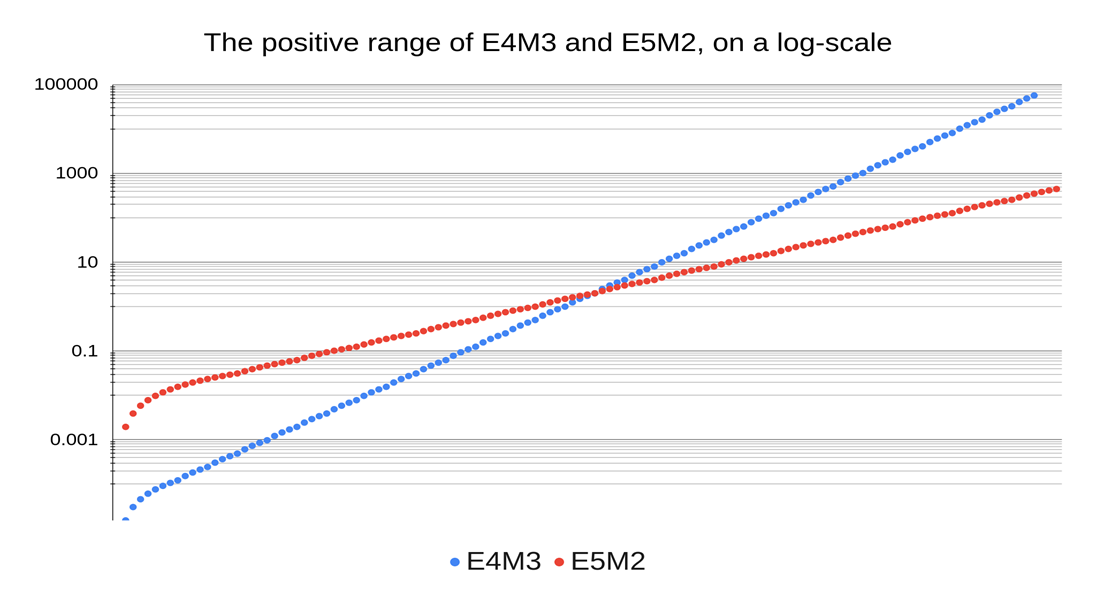
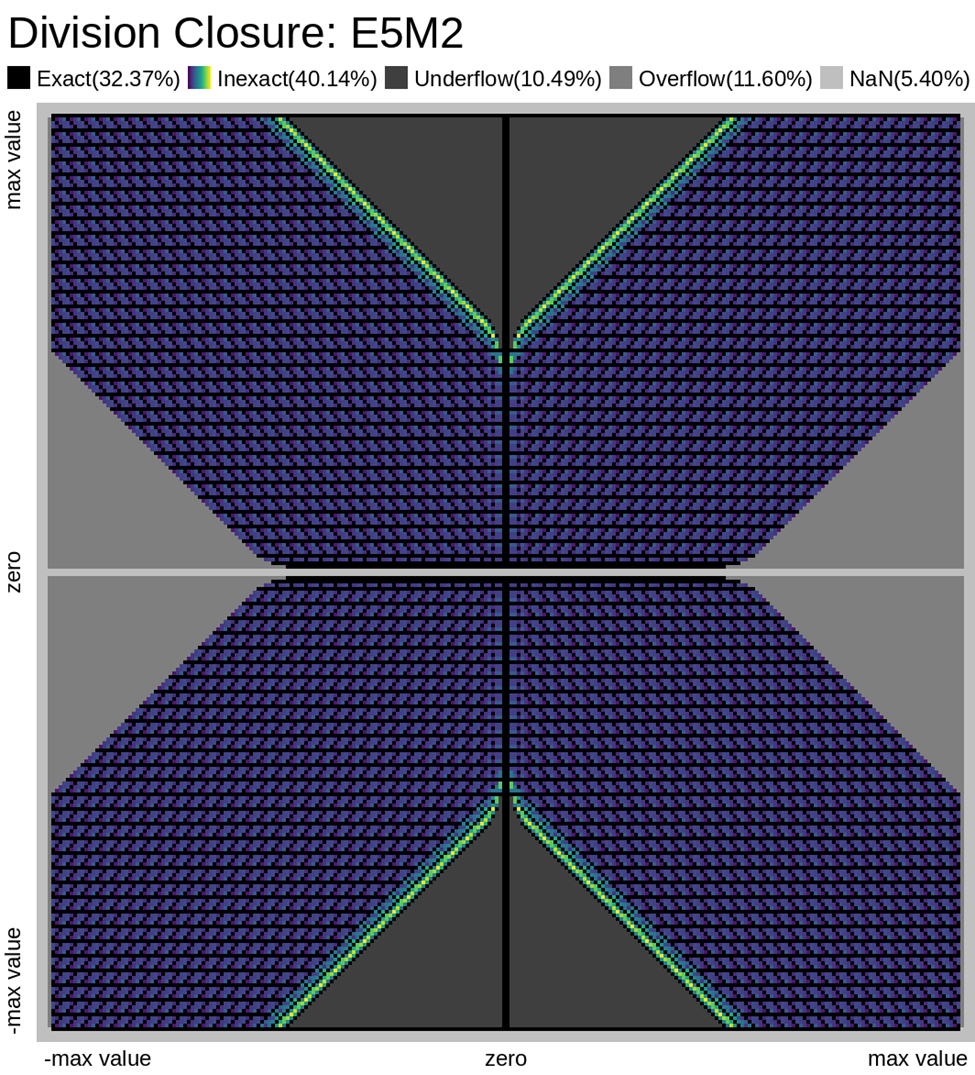
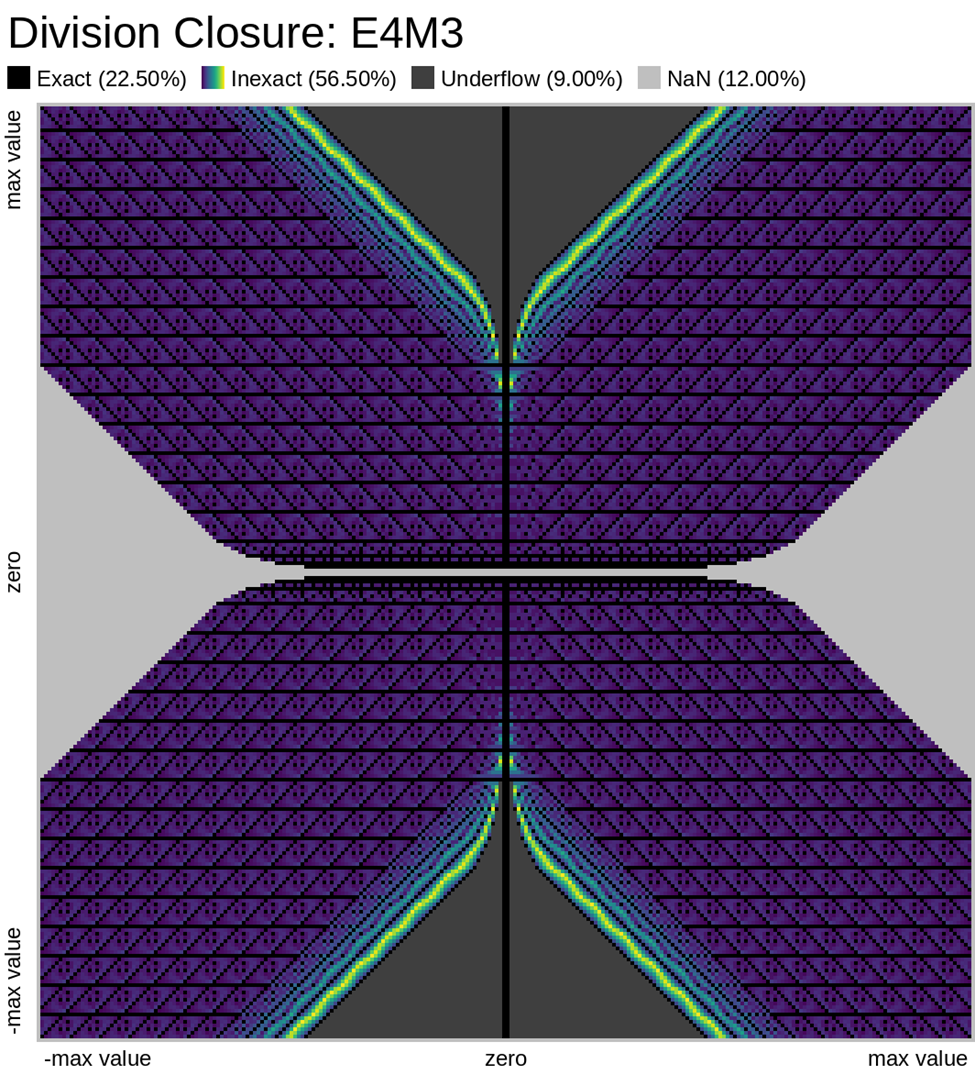
Error Plots
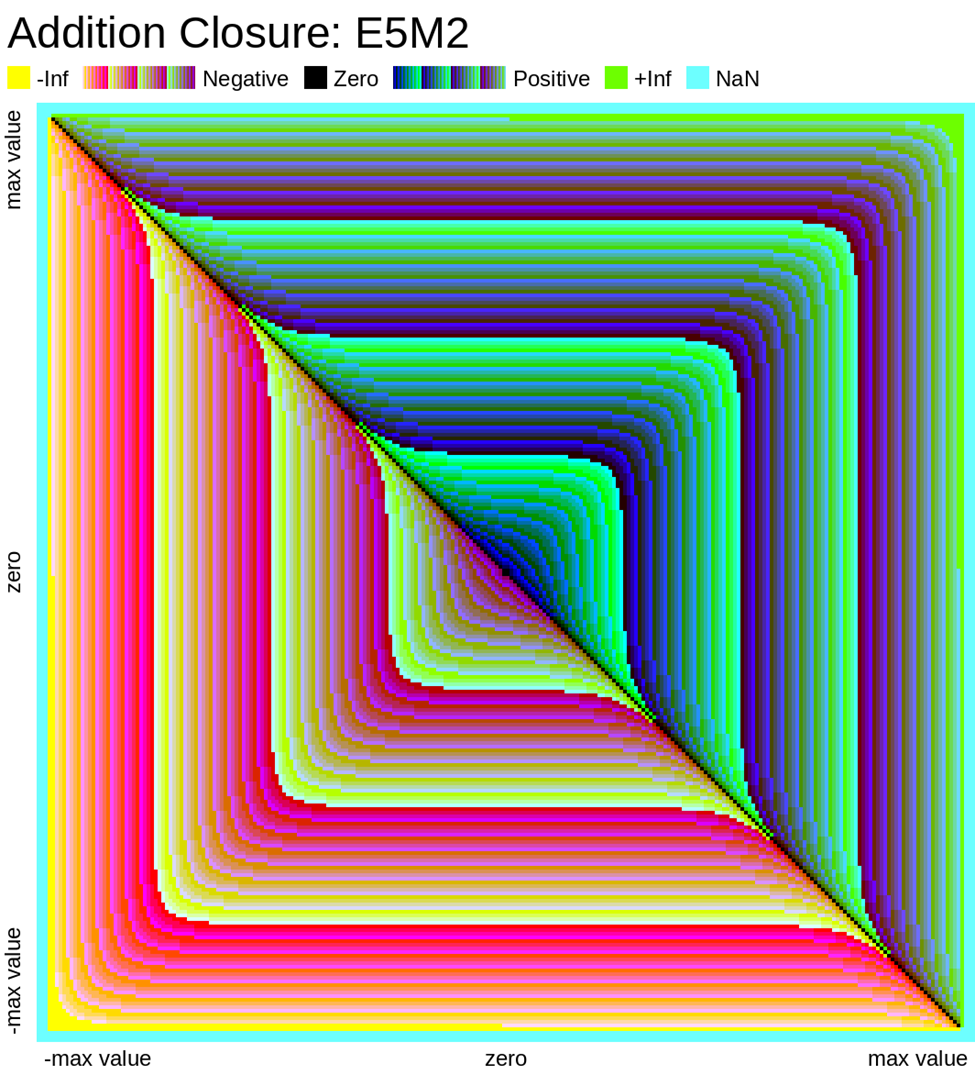
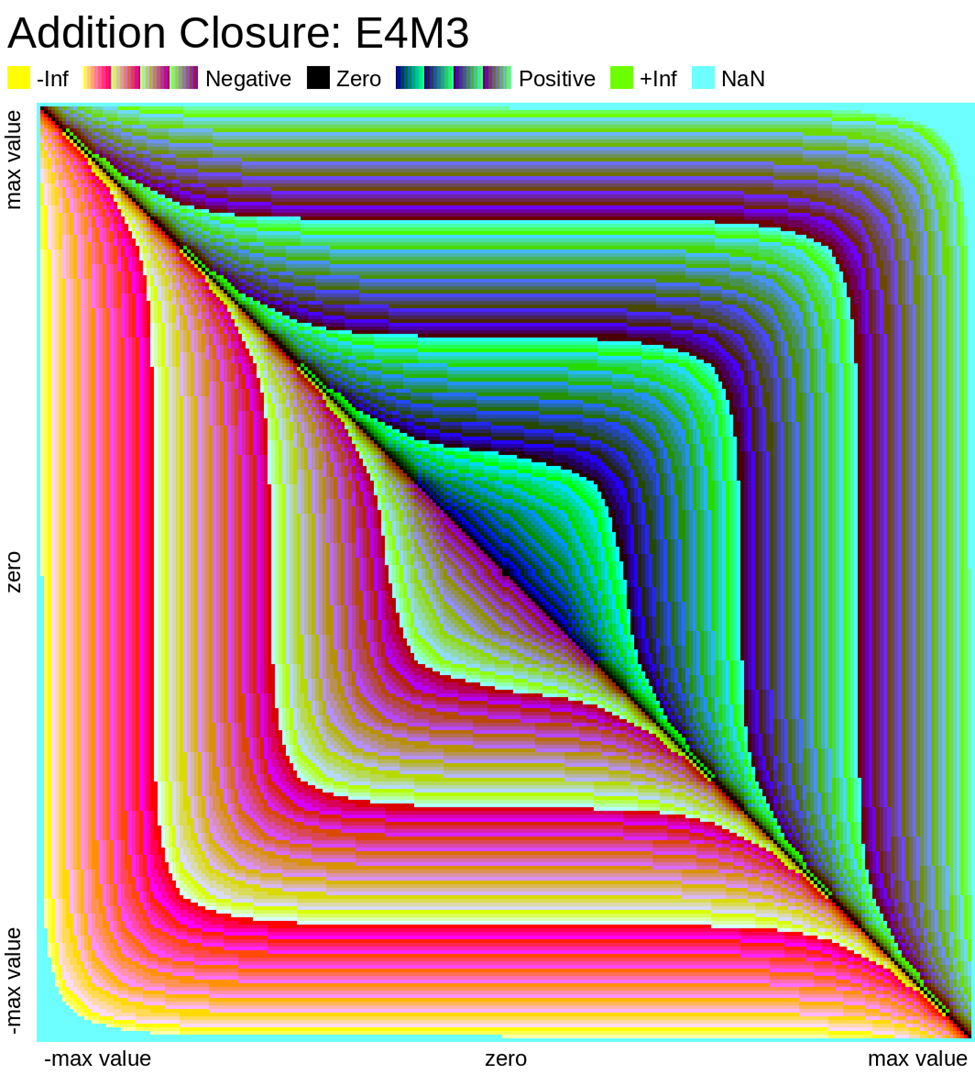
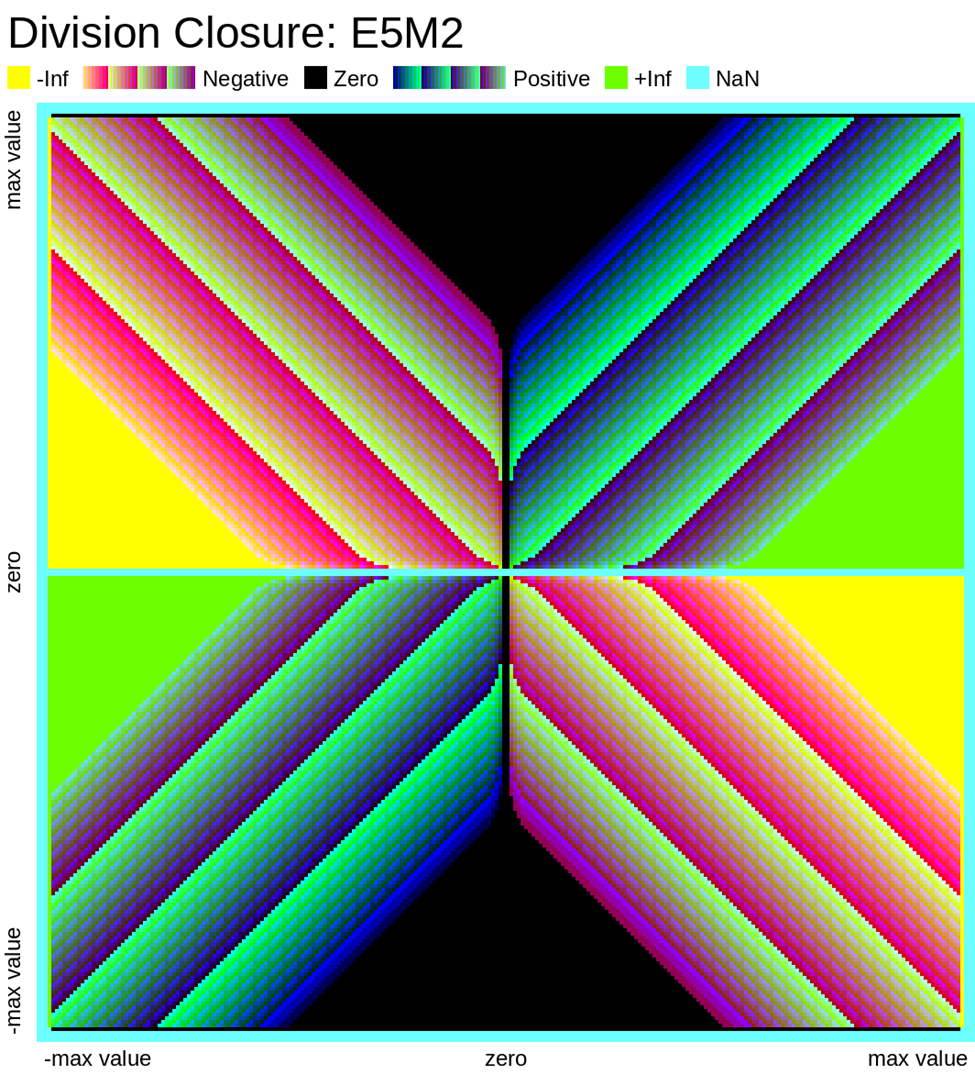
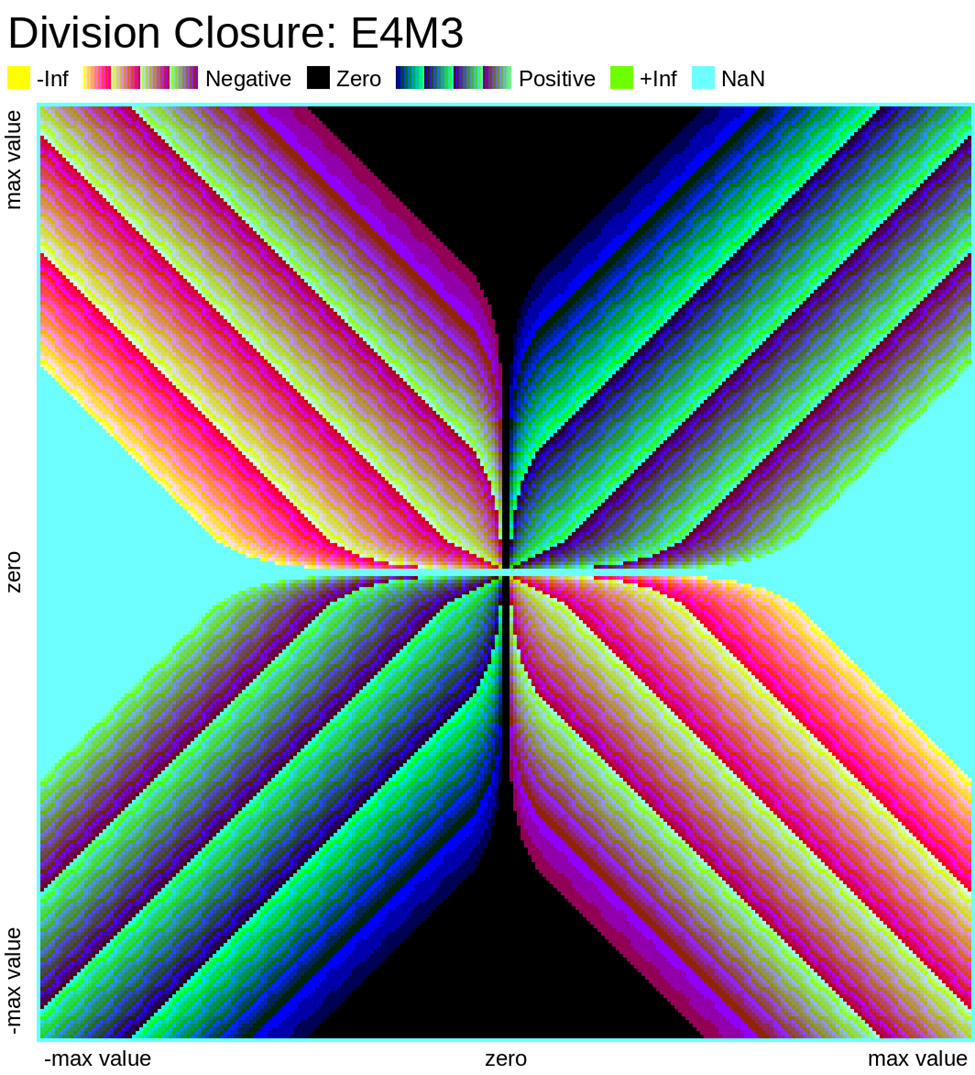
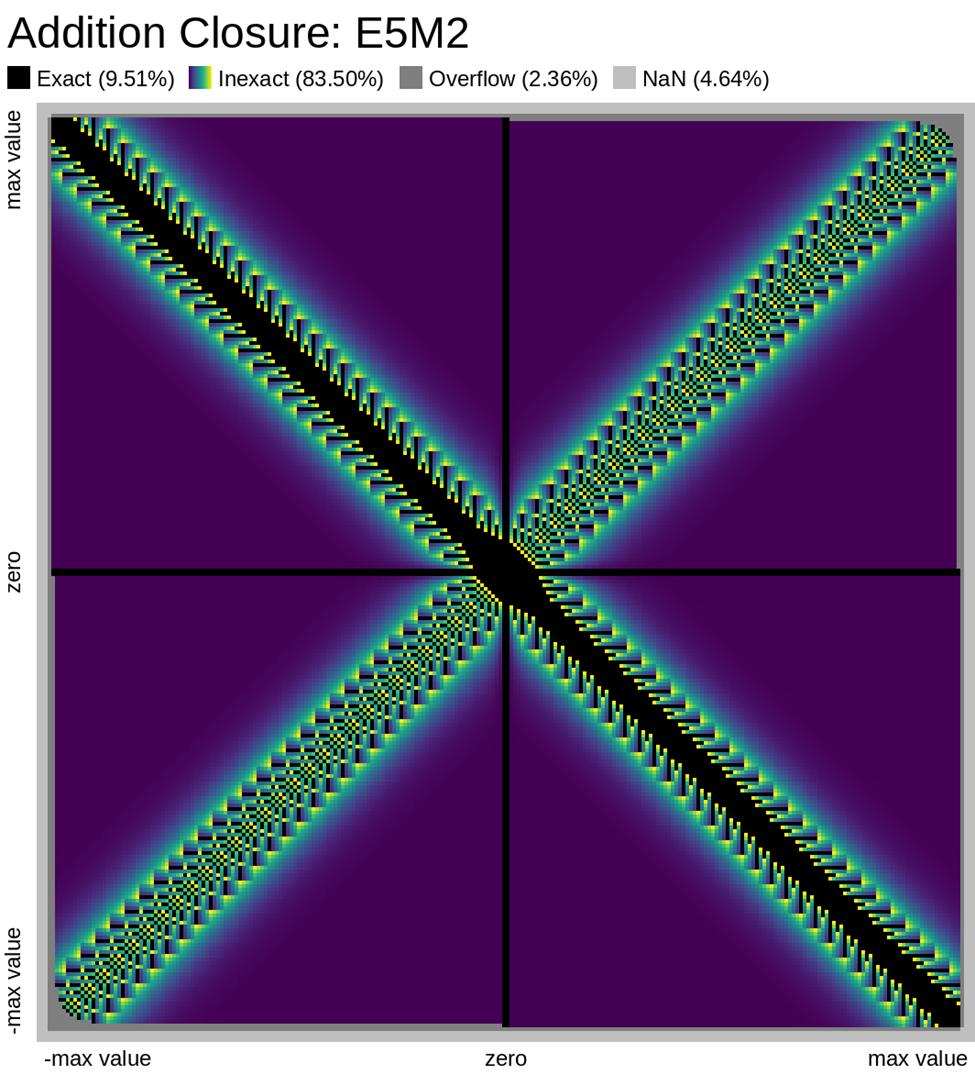
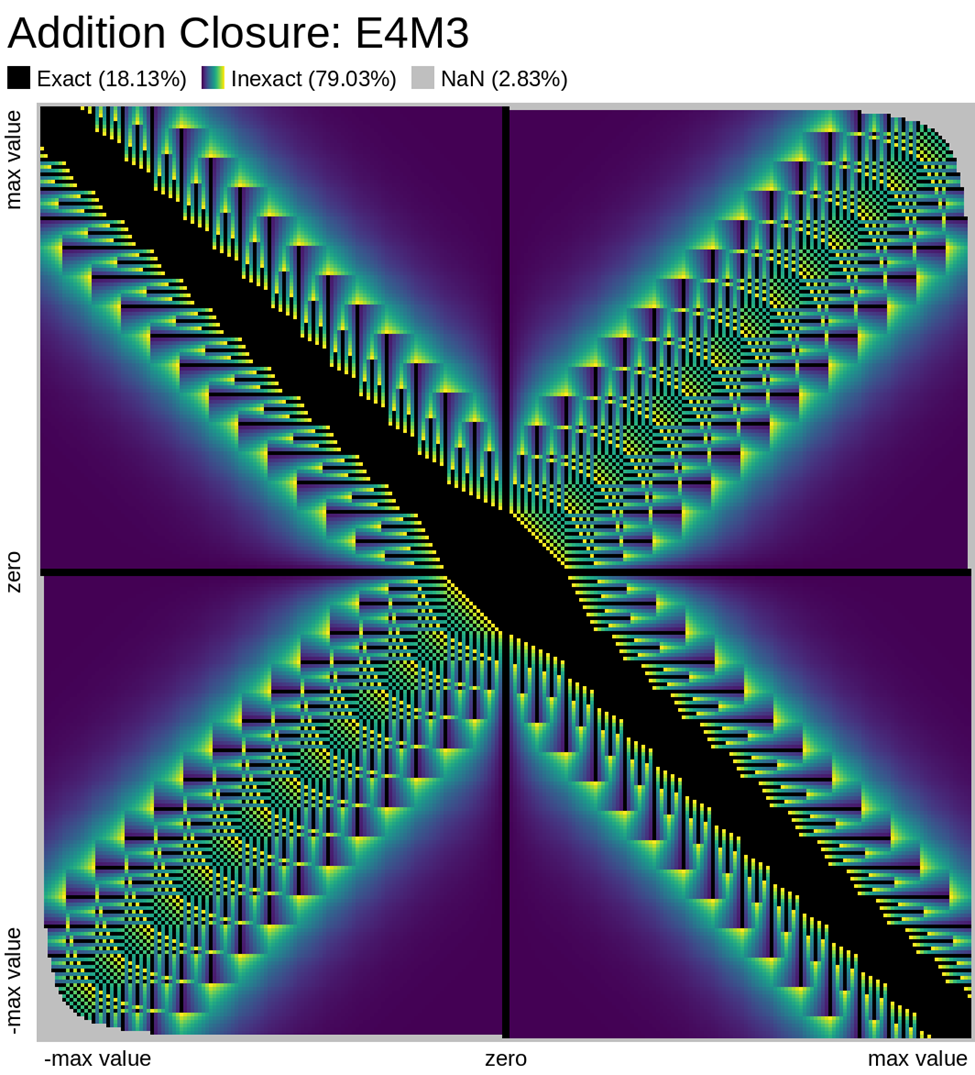
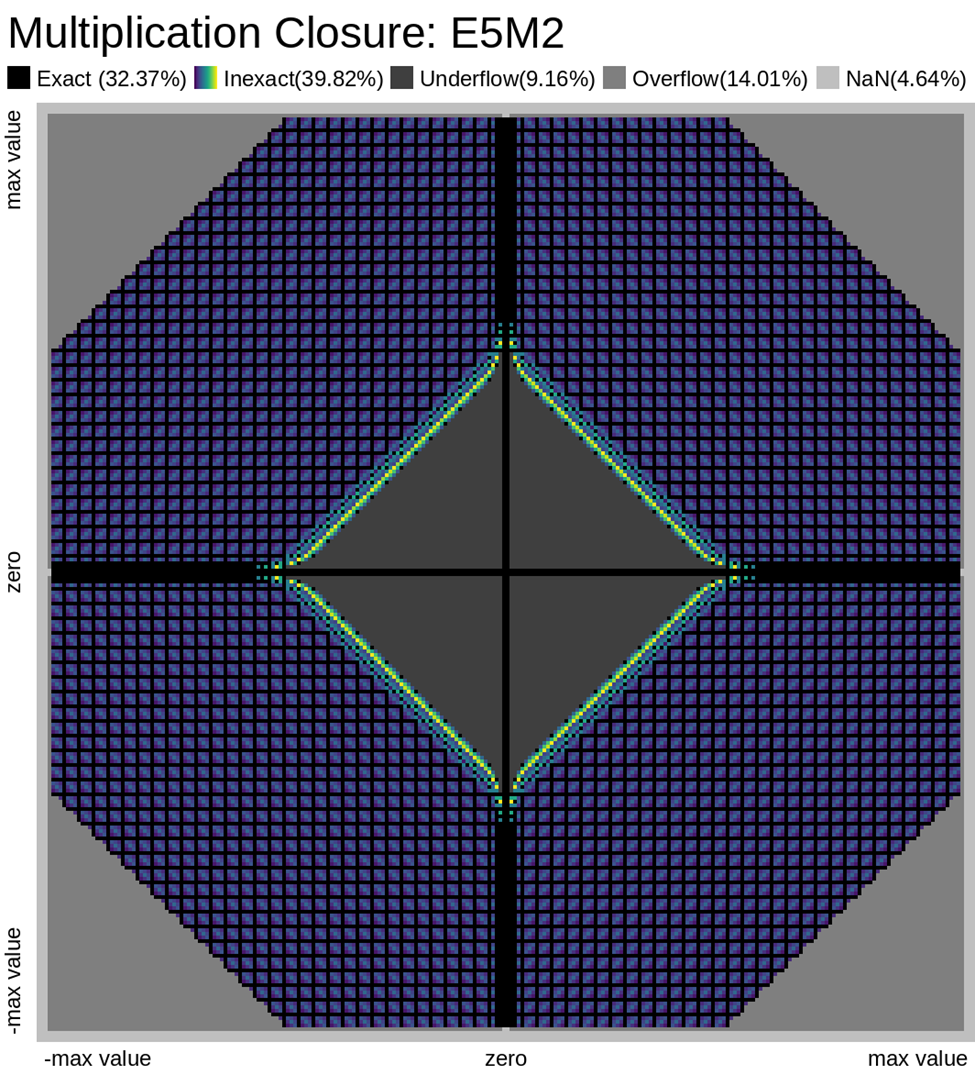
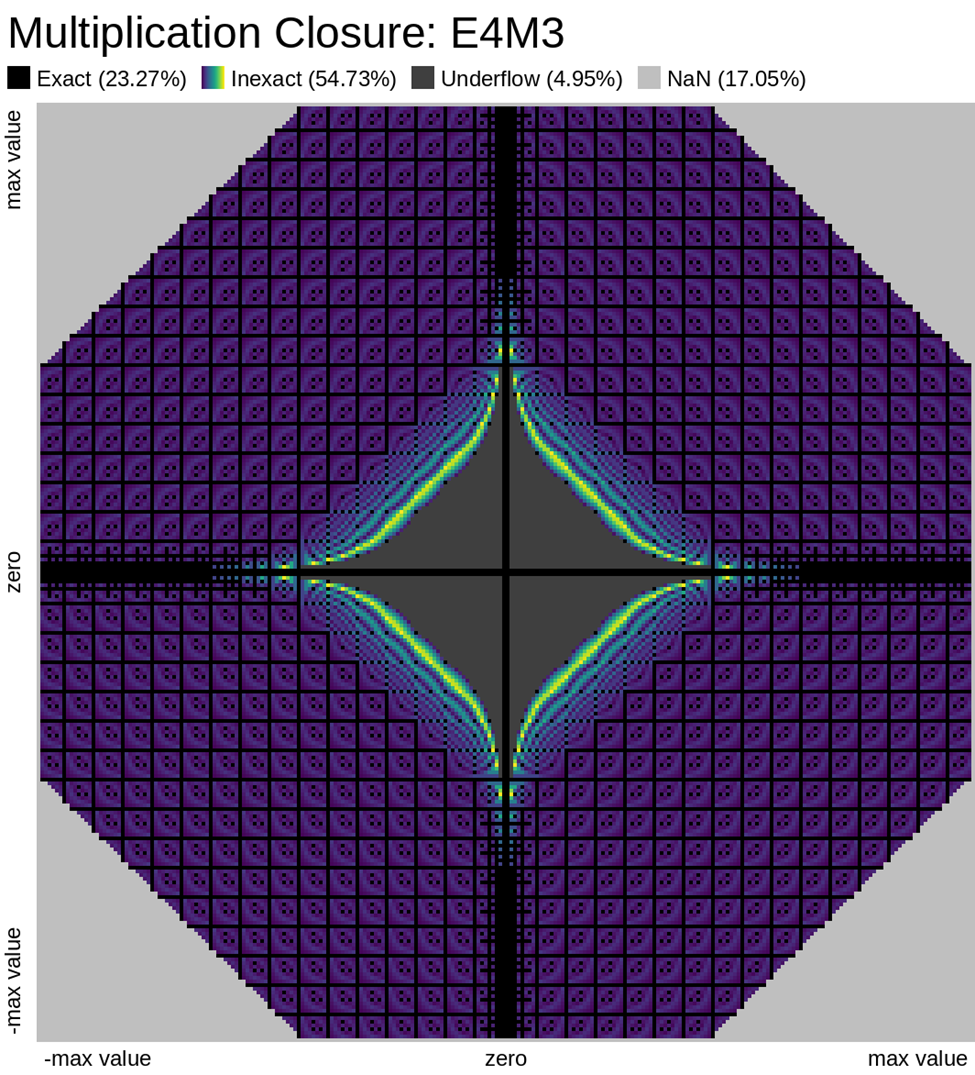
Here we look at some closure plots of operations in each of the two FP8 representations. Along the X and Y axes lay every number in the representation, including the special values such as -Inf, Inf, and Nan. For visual clarity, we place the representations with a negative sign bit on the left side, in the opposite direction.
We compute the op, and get the resulting value in the representation. Results which have an exact representation in the format are shown in black. For results that can't be represented exactly in the format, we show the relative error from least (dark purple) to most (bright yellow). Ops that result in +/- Infinity or “Not a Number” (NaN) are shown as well.
Results that underflow (are smaller than the smallest positive number) are treated differently. This is again for visual clarity but, in most implementations of the IEEE 754 specification, they round down to zero.
Also note that E4M3 does not have a representation of +/- Infinity, therefore, all values which would normally overflow to +/- Inf, are instead treated as NaN.
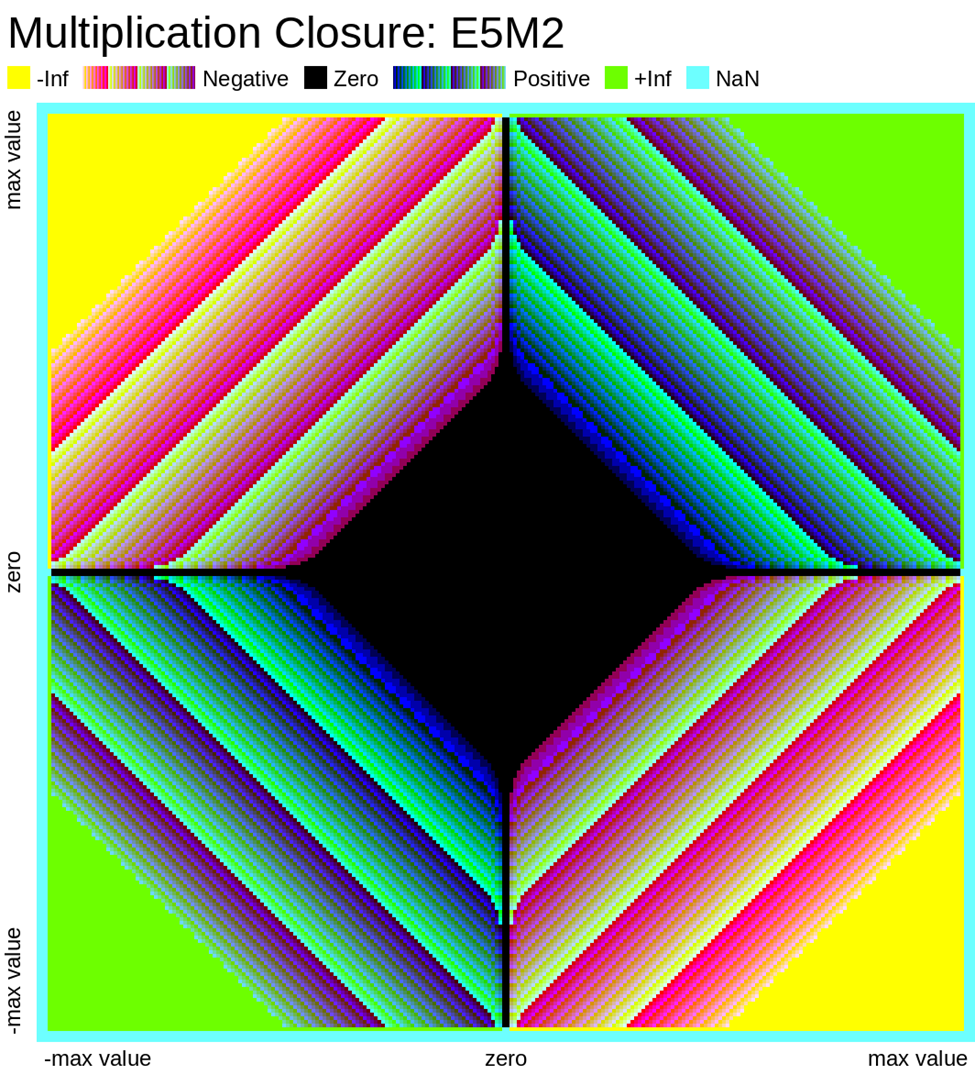
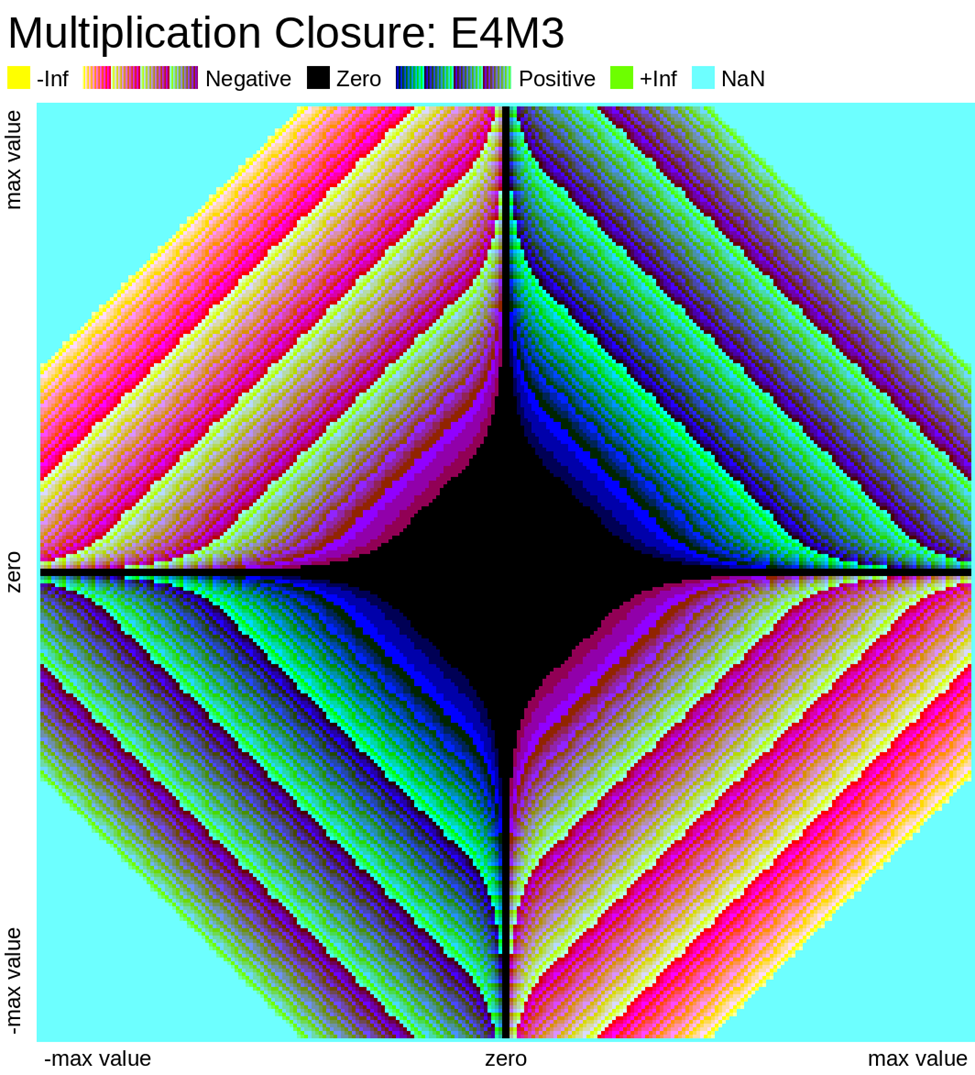
Value Plots
The following plots are similar to the above error closure plots, but instead show the value of the result of the operation in FP8. We map each 8-bit representation to 8-bit color values (3 bits for R, 3 bits for G, 2 bits for B)
Any values that underflow are rounded down to zero. We also choose to ignore the sign bit of zero and NaN, in order to present zero and special values in only one color. Again, we should note E4M3 has no representations for +/- Infinity, these values are represented instead as NaN.